Biodiversity The variability among living organisms from all sources including, inter alia, terrestrial, marine and other aquatic ecosystems and the ecological complexes of which they are part; this includes diversity within species, between species and of ecosystems.

— International Union for the Conservation of Nature (IUCN), Convention on Biological Diversity

The IUCN definition considers a diversity of diversity concepts. This module looks at diversity only at the species level (species diversity). However, we can also approach macroecological problems from phylogenetic and functional (and other) diversity concepts of view. Functional and phylogenetic diversity ideas will be introduced in the BDC743 module Quantitative Ecology.

Preparation

The South African Seaweed Data

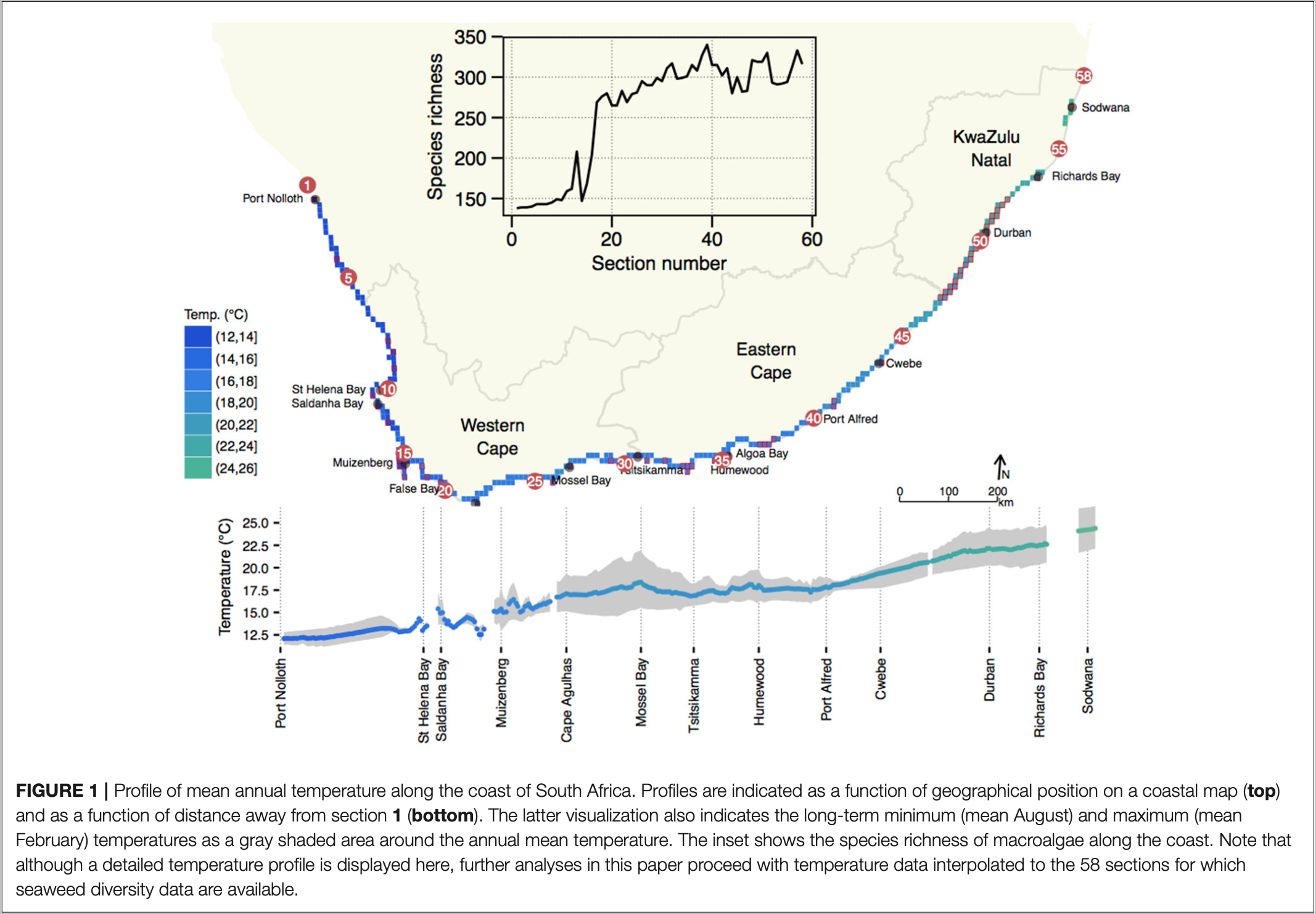
In these examples, we will use the seaweed data of Smit et al. (2017). Please make sure that you read this paper. An additional file describing the background to the data is available here (Figure 1).

Figure 1: The coastal sections and associated seawater temperature profile associated with the study by Smit et al. (2017).

One of the datasets, \(Y\) (in the file SeaweedSpp.csv), comprises updated distribution records of 847 macroalgal species within each of 58 × 50 km-long sections of the South African coast (Bolton and Stegenga 2002). The dataset captures ca. 90% of the known seaweed flora of South Africa, but excludes some very small and/or very rare species for which data are insufficient. The data are from verifiable literature sources and John Bolton and Rob Anderson’s collections, assembled from information collected by teams of phycologists over three decades (Bolton 1986; Stegenga et al. 1997; Bolton and Stegenga 2002; De Clerck et al. 2005). Another file, \(E\) (in env.csv), is a dataset of in situ coastal seawater temperatures derived from daily measurements over 40 years (Smit et al. 2013).

Setting Up the Analysis Environment

We will use R, so first, we must find, install and load various packages. Some packages will be available on CRAN and can be accessed and installed the usual way, but you will need to download others from R Forge.

library(tidyverse)
library(vegan)
library(betapart)
library(BiodiversityR) # this package may at times be problematic to install

A Look at the Data

Let’s load the data and see how it is structured:

spp <- read.csv('../data/seaweed/SeaweedSpp.csv')
spp <- dplyr::select(spp, -1)

# Lets look at the data:
dim(spp)

[1]  58 847

We see that our dataset has 58 rows and 847 columns. What is in the columns and rows? Start with the first five rows and five columns:

spp[1:5, 1:5]

  ACECAL ACEMOE ACRVIR AROSP1 ANAWRI
1      0      0      0      0      0
2      0      0      0      0      0
3      0      0      0      0      0
4      0      0      0      0      0
5      0      0      0      0      0

Now the last five rows and five columns:

spp[(nrow(spp) - 5):nrow(spp), (ncol(spp) - 5):ncol(spp)]

   WOMKWA WOMPAC WRAARG WRAPUR WURMIN ZONSEM
53      0      0      1      0      0      0
54      0      0      1      0      0      0
55      0      0      1      0      0      0
56      0      1      1      0      1      0
57      1      0      1      0      1      0
58      0      0      1      0      1      0

So, each row corresponds to a site (i.e. each of the coastal sections), and each column contains a species. We arrange the species alphabetically and use a six-letter code to identify them.

Species Data

When ecologists talk about species diversity, they typically consider the characteristics of biological communities in a specific habitat, ecological community, or ecosystem. Species diversity considers three essential concepts about how species are distributed in space: their richness, abundance, and evenness. We can express each of these as biodiversity metrics that allow us to compare communities in space and time.

When ecologists talk about ‘biodiversity’, they might not necessarily be interested in all the plants and animals and things that are neither plant nor animal that occur at a particular place. Some ecologists are interested in ants and moths. Others might find fish more insightful. Some even like marine mammals! I prefer seaweed. The analysis of biodiversity data might often be constrained to some higher-level taxon, such as all angiosperms in a landscape, reptiles, etc. (but we sample all species in the higher-level taxon). Some ecological questions benefit from comparisons of diversity assessments among selected taxa (avifauna vs small mammals, for example), as this focus might address some particular ecological hypothesis. The bird vs small mammal comparison might reveal how barriers such as streams and rivers structure biodiversity patterns. In our examples, we will use such focused datasets.

Here we look at the various measures of biodiversity, viz. \(\alpha\)-, \(\gamma\)- and \(\beta\)-diversity. David Zelený, in his Analysis of community data in R, provides deeper analysis and compulsory reading.

Three Measures of Biodiversity: \(\alpha\)-, \(\gamma\)-, \(\beta\)-Diversity

Whittaker (1972) coined three measures of biodiversity, and the concepts were ‘modernised’ by Jurasinski et al. (2009). The concepts represent the measurement of biodiversity across different spatial scales. \(\alpha\)- and \(\gamma\)-diversity express the total number of species in an area. The first, \(\alpha\)-diversity, represents the number of species at the small (local) scale, such as, for example, within a sampling unit like a quadrat, transect, plot, or trawl. Alternatively, maybe the research question represents the local scale by several sampling units nesting within a small patch of landscape and defines the mean species richness within this patch as local. Multiples (sampling units or patches) are nested within a larger region (or ecosystem) and serve as replicates. The complete number of species across all of these replicates indicates the diversity at a larger scale—this is called \(\gamma\)-diversity. \(\beta\)-diversity refers to the change in species composition among samples (sites).

By now, you will have received a brief Introduction to R, and we can proceed with looking at some of the measures of biodiversity. We will start by using data on the seaweeds of South Africa to demonstrate some ideas around diversity measures. The vegan¹ (for vegetation analysis) package (Oksanen et al. 2022) offers various functions to calculate diversity indices. I will demonstrate some of these functions below.

¹ I am by no means an advocate for veganism.

Alpha-Diversity

We can represent \(\alpha\)-diversity in three ways:

as species richness, \(S\);
as a univariate diversity index, such as the \(\alpha\) parameter of Fisher’s log-series, Shannon diversity, \(H'\), Simpson’s diversity, \(\lambda\); or
Species evenness, e.g. Pielou’s evenness, \(J\).

We will work through each in turn.

Species Richness, \(S\)

First, is species richness, which we denote by the symbol \(S\). This is the simplest measure of \(\alpha\)-diversity, counting the number of species (or another taxonomic level) present in a given community or sample. It doesn’t consider the abundance of species.

In the seaweed biodiversity data, I count the number of species within each of the sections. This is because we view each coastal section as the local scale (the smallest unit of sampling).

The preferred option for calculating species richness is the specnumber() function in vegan:

1specnumber(spp, MARGIN = 1)

1: The MARGIN = 1 argument tells R to calculate the number of species within each row (site).

 [1] 138 139 139 140 143 143 143 145 149 148 159 162 208 147 168 204 269 276 280
[20] 265 265 283 269 279 281 295 290 290 299 295 311 317 298 299 301 315 308 327
[39] 340 315 315 302 311 280 300 282 283 321 319 319 330 293 291 292 294 313 333
[58] 316

The data output is easier to understand if we display it as a tibble():

spp_richness <- tibble(section = 1:58,
                       richness = specnumber(spp, MARGIN = 1))
head(spp_richness)

# A tibble: 6 × 2
  section richness
    <int>    <int>
1       1      138
2       2      139
3       3      139
4       4      140
5       5      143
6       6      143

The diversityresult() function in the BiodiversityR package can do the same (sometimes this package is difficult to install due to various software dependencies that might be required for the package to load properly—do not be sad if this method does not work):

spp_richness <- diversityresult(spp, index = 'richness',
                                method = 'each site')
head(spp_richness)

Now we make a plot seen in Figure 2:

ggplot(data = spp_richness, (aes(x = 1:58, y = richness))) +
  geom_line(size = 1.2, colour = "indianred") +
  xlab("Coastal section, west to east") +
  ylab("Species richness") +
  theme_linedraw()

Figure 2: The seaweed species richness, \(S\), within each of the coastal sections along the shore of South Africa.

In other instances, it makes more sense to calculate the mean species richness of all the sampling units (e.g. quadrats) taken inside the ecosystem of interest. How you calculate and present species richness depend on your research question and so you will have to decide based on your data and study.

In the seaweed study, the mean ± SD species richness across all of the 58 coastal sections is:

round(mean(spp_richness$richness), 2)

[1] 259.24

round(sd(spp_richness$richness), 2)

[1] 68.03

Univariate Diversity Indices

The second way we can express \(\alpha\)-diversity is to use one of the univariate diversity indices. The choice of which index to use should be informed by the extent to which one wants to emphasise richness or evenness. Species richness, \(S\), does not consider evenness as it is all about richness (obviously). Simpson’s \(\lambda\) emphasises evenness a lot more. Shannon’s \(H'\) is somewhere in the middle.

Shannon’s \(H'\) is sometimes called Shannon’s diversity, the Shannon-Wiener index, the Shannon-Weaver index, or the Shannon entropy. This is a more nuanced measure that considers both species richness and evenness (how evenly individuals are distributed across different species).

It is calculated as:

\[H' = -\sum_{i=1}^{S} p_{i} \ln p_{i}\] where \(p_{i}\) is the proportion of individuals belonging to the \(i\)th species, and \(S\) is the species richness.

Simpson’s \(\lambda\), or simply the Simpson index, is a measure that represents the probability that two individuals randomly selected from a sample will belong to the same species. It is calculated as:

\[\displaystyle \lambda = \sum_{i=1}^{S} p_{i}^{2}\] where \(S\) is the species richness and \(p_{i}\) is the relative abundance of the \(i\)th species.

Fisher’s \(\alpha\) estimates the \(\alpha\) parameter of Fisher’s logarithmic series (see functions fisher.alpha() and fisherfit()). The estimation is possible only for actual counts (i.e. integers) of individuals, so it will not work for per cent cover, biomass, and other measures that real numbers can express. It’s especially useful for comparing the diversity of samples with different total abundances. We will get to this function later under Fisher’s logarithmic series.

Except for Fisher’s-\(\alpha\), we cannot calculate these for the seaweed data, because, in order to do so, we require abundance data—the seaweed data are presence-absence only. Let us load a fictitious dataset of the diversity of three different communities of plants, with each community corresponding to a different light environment (dim, mid, and high light):

light <- read.csv("../data/light_levels.csv")
light

        Site    A    B    C    D    E    F
1  low_light 0.75 0.62 0.24 0.33 0.21 0.14
2  mid_light 0.38 0.15 0.52 0.57 0.28 0.29
3 high_light 0.08 0.15 0.18 0.52 0.54 0.56

We can see above that instead of having data with 1s and 0s for presence-absence, here we have some values that indicate the relative number of individuals belonging to each of the species in the three light environments. We calculate species richness (as before), and also the Shannon and Simpson indices using vegan’s diversity() function:

light_div <- tibble(
  site = c("low_light", "mid_light", "high_light"),
  richness = specnumber(light[, 2:7], MARGIN = 1),
  shannon = round(diversity(light[, 2:7], MARGIN = 1, index = "shannon"), 2),
  simpson = round(diversity(light[, 2:7], MARGIN = 1, index = "simpson"), 2)
)
light_div

# A tibble: 3 × 4
  site       richness shannon simpson
  <chr>         <int>   <dbl>   <dbl>
1 low_light         6    1.62    0.78
2 mid_light         6    1.71    0.81
3 high_light        6    1.59    0.77

Evenness refers to the shape of a species abundance distribution, which suggests the relative abundance of different species.

One index for evenness is Pielou’s evenness, \(J\):

\[J = \frac{H^{\prime}} {log(S)}\]

where \(H'\) is Shannon’s diversity index, and \(S\) the number of species (i.e. \(S\)).

To calculate Pielou’s evenness index for the light data, we can do this:

H <- diversity(light[, 2:7], MARGIN = 1, index = "shannon")

J <- H/log(specnumber(light[, 2:7]))
round(J, 2)

[1] 0.91 0.95 0.89

Berger-Parker Index indicates the proportion of the community that the most abundant species represents. It is given by the formula:

\[d = \frac{N_{max}}{N}\] where \(N_{max}\) is the number of individuals of the most common species and \(N\) is the total number of individuals in the sample.

Chao1 and ACE are estimators often used to predict the total species richness in a community based on the number of rare species observed in samples.

Gamma-Diversity

Returning to the seaweed data, \(Y\), let us now look at \(\gamma\)-diversity—this would be the total number of species along the South African coastline in all 58 coastal sections. Since each column represents one species, and the dataset contains data collected at each of the 58 sites (the number of rows), we can do:

1ncol(spp)

1: The number of columns gives the total number of species in this example.

[1] 847

We can also use:

diversityresult(spp, index = 'richness', method = 'pooled')

       richness
pooled      846

Lab 3

(To be reviewed by BCB743 student but not for marks)

Why is there a difference between the two?
Which is correct?

Think before you calculate \(\gamma\)-diversity for your own data as it might not be as simple as here!

Beta-Diversity

Whittaker’s \(\beta\)-Diversity

The first measure of \(\beta\)-diversity comes from Whittaker (1960) and is called true \(\beta\)-diversity. In this instance, divide the \(\gamma\)-diversity for the region by the \(\alpha\)-diversity for a specific coastal section. We can calculate it all at once for the whole dataset and make a graph (Figure 3):

true_beta <- data.frame(
  beta = specnumber(spp, MARGIN = 1) / ncol(spp),
  section_no = c(1:58)
)
# true_beta
ggplot(data = true_beta, (aes(x = section_no, y = beta))) +
  geom_line(size = 1.2, colour = "indianred") +
  xlab("Coastal section, west to east") +
  ylab("True beta-diversity") +
  theme_linedraw()

Figure 3: Whittaker’s true β-diversity shown in the seaweed data.

The second measure of \(\beta\)-diversity is absolute species turnover, and to calculate this, we subtract \(\alpha\)-diversity for each section from the region’s \(\gamma\)-diversity (Figure 4):

abs_beta <- data.frame(
  beta = ncol(spp) - specnumber(spp, MARGIN = 1),
  section_no = c(1:58)
)
# abs_beta
ggplot(data = abs_beta, (aes(x = section_no, y = beta))) +
  geom_line(size = 1.2, colour = "indianred") +
  xlab("Coastal section, west to east") +
  ylab("Absolute beta-diversity") +
  theme_linedraw()

Figure 4: Whittaker’s absolute species turnover shown in action in the seaweed data.

Contemporary Definitions \(\beta\)-Diversity

Contemporary definitions of \(\beta\)-diversity rely on pairwise dissimilarity indices such as Bray-Curtis, Jaccard, or Sørensen dissimilarities—see Koleff et al. (2003) for many more; also see ?vegdist. However, discussing pairwise dissimilarities with \(\beta\)-diversity makes more sense.

Dissimilarity indices

Dissimilarity indices are special cases of diversity indices that use pairwise comparisons between sampling units, habitats, or ecosystems.

Species dissimilarities result in pairwise matrices similar to the pairwise correlation or Euclidian distance matrices we have seen in Lab 1. In Lab 2b you will have also learned how to calculate these ecological distances in R. These dissimilarity indices are multivariate and compare between sites, sections, plots, etc., and must therefore not be confused with the univariate diversity indices.

We use the Bray-Curtis and Jaccard indices with abundance data and the Sørensen dissimilarity with presence-absence data. The seaweed dataset is a presence-absence dataset that necessitates using the Sørensen index. The interpretation of the resulting square (number of rows = number of columns) dissimilarity matrices is the same regardless of whether we calculate it for an abundance or presence-absence dataset. The values in the matrix range from 0 to 1. A 0 means that the pair of sites we compare is identical (all species in common) but 1 means they are completely different (no species in common). In the square dissimilarity matrix, the diagonal is 0, which essentially (and obviously) means that any site is identical to itself. Elsewhere the values will range from 0 to 1. Since this is a pairwise calculation (each site compared to every other site), our seaweed dataset will contain (58 × (58 - 1))/2 = 1653 values, each one ranging from 0 to 1.

The first step involves the species table, \(Y\). First, we compute the Sørensen dissimilarity index, \(\beta_{\text{sør}}\), to compare the dissimilarity of all pairs of coastal sections using presence-absence data. The dissimilarity in species composition between two sections is calculated from three parameters, viz., b and c, which represent the number of species unique to each of the two sites, and a, the number of species in common between them. It is given by:

\[\beta_\text{sør}=\frac{2a}{2a+b+c}\] Where \(a\) is the number of species in common between two sites, and \(b\) and \(c\) are the number of species unique to each site. The Sørensen dissimilarity index ranges from 0 to 1, where 0 means that the pair of sites we compare is identical (all species in common) and 1 means they are completely different (no species in common).

The vegan function vegdist() provides access to the dissimilarity indices. We calculate the Sørensen dissimilarity index:

sor <- vegdist(spp, binary = TRUE) # makes the lower triangle matrix
sor_df <- round(as.matrix(sor), 4)
dim(sor_df)

[1] 58 58

sor_df[1:10, 1:10] # the first 10 rows and columns

        1      2      3      4      5      6      7      8      9     10
1  0.0000 0.0036 0.0036 0.0072 0.0249 0.0391 0.0391 0.0459 0.0592 0.0629
2  0.0036 0.0000 0.0000 0.0036 0.0213 0.0355 0.0355 0.0423 0.0556 0.0592
3  0.0036 0.0000 0.0000 0.0036 0.0213 0.0355 0.0355 0.0423 0.0556 0.0592
4  0.0072 0.0036 0.0036 0.0000 0.0177 0.0318 0.0318 0.0386 0.0519 0.0556
5  0.0249 0.0213 0.0213 0.0177 0.0000 0.0140 0.0140 0.0208 0.0342 0.0378
6  0.0391 0.0355 0.0355 0.0318 0.0140 0.0000 0.0000 0.0069 0.0205 0.0241
7  0.0391 0.0355 0.0355 0.0318 0.0140 0.0000 0.0000 0.0069 0.0205 0.0241
8  0.0459 0.0423 0.0423 0.0386 0.0208 0.0069 0.0069 0.0000 0.0136 0.0171
9  0.0592 0.0556 0.0556 0.0519 0.0342 0.0205 0.0205 0.0136 0.0000 0.0034
10 0.0629 0.0592 0.0592 0.0556 0.0378 0.0241 0.0241 0.0171 0.0034 0.0000

What we see above is a square dissimilarity matrix. The most important characteristics of the matrix are:

whereas the raw species data, \(Y\), is rectangular (number rows ≠ number columns), the dissimilarity matrix is square (number rows = number columns);
the diagonal is filled with 0;
the matrix is symmetrical—it is comprised of symetrical upper and lower triangles.

Create a data.frame suitable for plotting:

sor_df <- data.frame(round(as.matrix(sor), 4))

Lab 3

(To be reviewed by BCB743 student but not for marks)

These questions concern matrices produced from species data using any of the indices available in vegdist():

Why is the matrix square, and what determines the number of rows/columns?
What is the meaning of the diagonal?
What is the meaning of the non-diagonal elements?
Referring to the seaweed species data specifically, take the data in row 1 or column 1 and create a line graph showing these values as a function of the section number.
Provide a mechanistic (ecological) explanation for why this figure takes the shape that it does. Which community assembly process does this hint at?

There are different interpretations linked to \(\beta\)-diversity, each telling us something different about community formation processes.

Species turnover and nestedness-resultant \(\beta\)-diversity

There are two kinds of \(\beta\)-diversity: species turnover and nestedness-resultant \(\beta\)-diversity. The former is the result of species replacement between sites, whereas the latter is the result of species loss or gain between sites. The Sørensen dissimilarity index, \(\beta_\text{sør}\), can be decomposed into these two components.

How do we calculate the turnover and nestedness-resultant components of \(\beta\)-diversity? The betapart package (Baselga et al. 2022) comes to the rescue. We decompose the dissimilarity into the \(\beta_\text{sim}\) and \(\beta_\text{sne}\) components (Baselga 2010) using the betapart.core() and betapart.pair() functions. The outcomes of this partitioning calculation are placed into the matrices \(Y1\) and \(Y2\). These data can then be analysed further—e.g. we can apply a principal components analysis (PCA) or another multivariate analysis on \(Y\) to find the major patterns in the community data—we will do this in BCB743.

# Decompose total Sørensen dissimilarity into turnover and nestedness-resultant
# components:
Y.core <- betapart.core(spp)
Y.pair <- beta.pair(Y.core, index.family = "sor")

# Let Y1 be the turnover component (beta-sim):
Y1 <- data.frame(round(as.matrix(Y.pair$beta.sim), 3))

# Let Y2 be the nestedness-resultant component (beta-sne):
Y2 <- data.frame(round(as.matrix(Y.pair$beta.sne), 3))

A portion of the turnover component matrix:

Y1[1:10, 1:10]

      X1    X2    X3    X4    X5    X6    X7    X8    X9   X10
1  0.000 0.000 0.000 0.000 0.007 0.022 0.022 0.022 0.022 0.029
2  0.000 0.000 0.000 0.000 0.007 0.022 0.022 0.022 0.022 0.029
3  0.000 0.000 0.000 0.000 0.007 0.022 0.022 0.022 0.022 0.029
4  0.000 0.000 0.000 0.000 0.007 0.021 0.021 0.021 0.021 0.029
5  0.007 0.007 0.007 0.007 0.000 0.014 0.014 0.014 0.014 0.021
6  0.022 0.022 0.022 0.021 0.014 0.000 0.000 0.000 0.000 0.007
7  0.022 0.022 0.022 0.021 0.014 0.000 0.000 0.000 0.000 0.007
8  0.022 0.022 0.022 0.021 0.014 0.000 0.000 0.000 0.000 0.007
9  0.022 0.022 0.022 0.021 0.014 0.000 0.000 0.000 0.000 0.000
10 0.029 0.029 0.029 0.029 0.021 0.007 0.007 0.007 0.000 0.000

A portion of the nestedness-resultant matrix:

Y2[1:10, 1:10]

      X1    X2    X3    X4    X5    X6    X7    X8    X9   X10
1  0.000 0.004 0.004 0.007 0.018 0.017 0.017 0.024 0.037 0.034
2  0.004 0.000 0.000 0.004 0.014 0.014 0.014 0.021 0.034 0.030
3  0.004 0.000 0.000 0.004 0.014 0.014 0.014 0.021 0.034 0.030
4  0.007 0.004 0.004 0.000 0.011 0.010 0.010 0.017 0.030 0.027
5  0.018 0.014 0.014 0.011 0.000 0.000 0.000 0.007 0.020 0.017
6  0.017 0.014 0.014 0.010 0.000 0.000 0.000 0.007 0.021 0.017
7  0.017 0.014 0.014 0.010 0.000 0.000 0.000 0.007 0.021 0.017
8  0.024 0.021 0.021 0.017 0.007 0.007 0.007 0.000 0.014 0.010
9  0.037 0.034 0.034 0.030 0.020 0.021 0.021 0.014 0.000 0.003
10 0.034 0.030 0.030 0.027 0.017 0.017 0.017 0.010 0.003 0.000

A portion of the nestedness-resultant matrix reformatted as a tibble()²:

² Note that the rows are no longer numbered in the tibble view, but it can easily be recreated by seq(1:58).

Y2_tib <- as_tibble(Y2)
head(Y2_tib)

# A tibble: 6 × 58
     X1    X2    X3    X4    X5    X6    X7    X8    X9   X10   X11   X12   X13
  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0     0.004 0.004 0.007 0.018 0.017 0.017 0.024 0.037 0.034 0.069 0.078 0.196
2 0.004 0     0     0.004 0.014 0.014 0.014 0.021 0.034 0.03  0.065 0.074 0.193
3 0.004 0     0     0.004 0.014 0.014 0.014 0.021 0.034 0.03  0.065 0.074 0.193
4 0.007 0.004 0.004 0     0.011 0.01  0.01  0.017 0.03  0.027 0.062 0.071 0.19 
5 0.018 0.014 0.014 0.011 0     0     0     0.007 0.02  0.017 0.052 0.061 0.181
6 0.017 0.014 0.014 0.01  0     0     0     0.007 0.021 0.017 0.053 0.062 0.184
# ℹ 45 more variables: X14 <dbl>, X15 <dbl>, X16 <dbl>, X17 <dbl>, X18 <dbl>,
#   X19 <dbl>, X20 <dbl>, X21 <dbl>, X22 <dbl>, X23 <dbl>, X24 <dbl>,
#   X25 <dbl>, X26 <dbl>, X27 <dbl>, X28 <dbl>, X29 <dbl>, X30 <dbl>,
#   X31 <dbl>, X32 <dbl>, X33 <dbl>, X34 <dbl>, X35 <dbl>, X36 <dbl>,
#   X37 <dbl>, X38 <dbl>, X39 <dbl>, X40 <dbl>, X41 <dbl>, X42 <dbl>,
#   X43 <dbl>, X44 <dbl>, X45 <dbl>, X46 <dbl>, X47 <dbl>, X48 <dbl>,
#   X49 <dbl>, X50 <dbl>, X51 <dbl>, X52 <dbl>, X53 <dbl>, X54 <dbl>, …

Lab 3 (continue)

(To be reviewed by BCB743 student but not for marks)

Plot species turnover as a function of Section number, and provide a mechanistic explanation for the pattern observed.
Based on an assessment of literature on the topic, provide a discussion of nestedness-resultant \(\beta\)-diversity. Use either a marine or terrestrial example to explain this mode of structuring biodiversity (i.e. assembly of species into a community).

Submission Instructions

The Lab 3 assignment is due at 07:00 on Monday 12 August 2022.

Provide a neat and thoroughly annotated R file which can recreate all the graphs and all calculations. Written answers must be typed in the same file as comments.

Please label the R file as follows:

BDC334_<first_name>_<last_name>_Lab_3.R

(the < and > must be omitted as they are used in the example as field indicators only).

Submit your appropriately named R documents on iKamva when ready.

Failing to follow these instructions carefully, precisely, and thoroughly will cause you to lose marks, which could cause a significant drop in your score as formatting counts for 15% of the final mark (out of 100%).

References

Baselga A (2010) Partitioning the turnover and nestedness components of beta diversity. Global Ecology and Biogeography 19:134–143.

Baselga A, Orme D, Villeger S, De Bortoli J, Leprieur F, Logez M (2022) betapart: Partitioning Beta Diversity into Turnover and Nestedness Components.

Bolton J (1986) Marine phytogeography of the Benguela upwelling region on the west coast of southern africa: A temperature dependent approach.

Bolton J, Stegenga H (2002) Seaweed species diversity in South Africa. South African Journal of Marine Science 24:9–18.

De Clerck O, Bolton J, Anderson R, Coppejans E, Bolton J, Anderson R (2005) Guide to the seaweeds of KwaZulu-Natal.

Jurasinski G, Retzer V, Beierkuhnlein C (2009) Inventory, differentiation, and proportional diversity: A consistent terminology for quantifying species diversity. Oecologia 159:15–26.

Koleff P, Gaston KJ, Lennon JJ (2003) Measuring beta diversity for presence–absence data. Journal of Animal Ecology 72:367–382.

Oksanen J, Simpson GL, Blanchet FG, Kindt R, Legendre P, Minchin PR, O’Hara RB, Solymos P, Stevens MHH, Szoecs E, Wagner H, Barbour M, Bedward M, Bolker B, Borcard D, Carvalho G, Chirico M, De Caceres M, Durand S, Evangelista HBA, FitzJohn R, Friendly M, Furneaux B, Hannigan G, Hill MO, Lahti L, McGlinn D, Ouellette M-H, Ribeiro Cunha E, Smith T, Stier A, Ter Braak CJF, Weedon J (2022) vegan: Community Ecology Package.

Smit AJ, Roberts M, Anderson RJ, Dufois F, Dudley SF, Bornman TG, Olbers J, Bolton JJ (2013) A coastal seawater temperature dataset for biogeographical studies: large biases between in situ and remotely-sensed data sets around the coast of South Africa. PLoS One 8:e81944.

Smit AJ, Bolton JJ, Anderson RJ (2017) Seaweeds in two oceans: Beta-diversity. Frontiers in Marine Science 4:404.

Stegenga H, Bolton JJ, Anderson RJ (1997) Seaweeds of the South African west coast.

Whittaker RH (1960) Vegetation of the Siskiyou mountains, Oregon and California. Ecological Monographs 30:279–338.

Whittaker RH (1972) Evolution and measurement of species diversity. Taxon 21:213–251.

Reuse

CC BY-NC-SA 4.0

Citation

BibTeX citation:

@online{j._smit2021,
  author = {J. Smit, Albertus},
  title = {Lab 3. {Quantifying} {Biodiversity}},
  date = {2021-01-01},
  url = {http://tangledbank.netlify.app/BDC334/03-biodiversity1.html},
  langid = {en}
}

For attribution, please cite this work as:

J. Smit A (2021) Lab 3. Quantifying Biodiversity. http://tangledbank.netlify.app/BDC334/03-biodiversity1.html.