Lecture 2b: Metrics of Environmental Distance & Species Diversity
This material must be reviewed by BCB743 students in Week 1 of Quantitative Ecology.
Quantifying Diversity
When we talk about ‘biodiversity,’ we typically refer to the variety of life in a given area or ecosystem. This encompasses species diversity, genetic diversity within species, and the diversity of ecosystems or habitats. To quantify biodiversity, we use metrics that capture various aspects, including:
- The variability and characteristics of the environment.
- The species present in a given area (species lists).
- The relative abundance of each of the species.
- The spatial distribution of species across different habitats or ecosystems.
In this lecture, we will explore some of the most common metrics used to quantify biodiversity. We’ll delve into the concepts of species richness, evenness, and diversity, and how these metrics can be applied to compare different habitats or ecosystems.
Biodiversity metrics can be broadly categorised into three groups based on the type of information they provide:
- Biodiversity metrics (\alpha-diversity, \beta-diversity, \gamma-diversity).
- Diversity indices (e.g., Shannon’s Entropy, Gini Index, Herfindahl-Hirschman Index (HHI)).
- Distance measures (e.g., Euclidean, Manhattan) and Dissimilarity indices (e.g., Bray-Curtis, Jaccard, Sørensen).
The first two categories—biodiversity metrics and diversity indices—offer simplified representations of biodiversity through synthetic metrics or indices. In contrast, distance measures and dissimilarity indices provide more nuanced and detailed insights by exposing the full multivariate information within our datasets. This allows for a deeper examination of the processes driving community formation and the resulting structures that describe biodiversity patterns across landscapes.
Biodiversity Metrics
\alpha-Diversity (Species Richness)
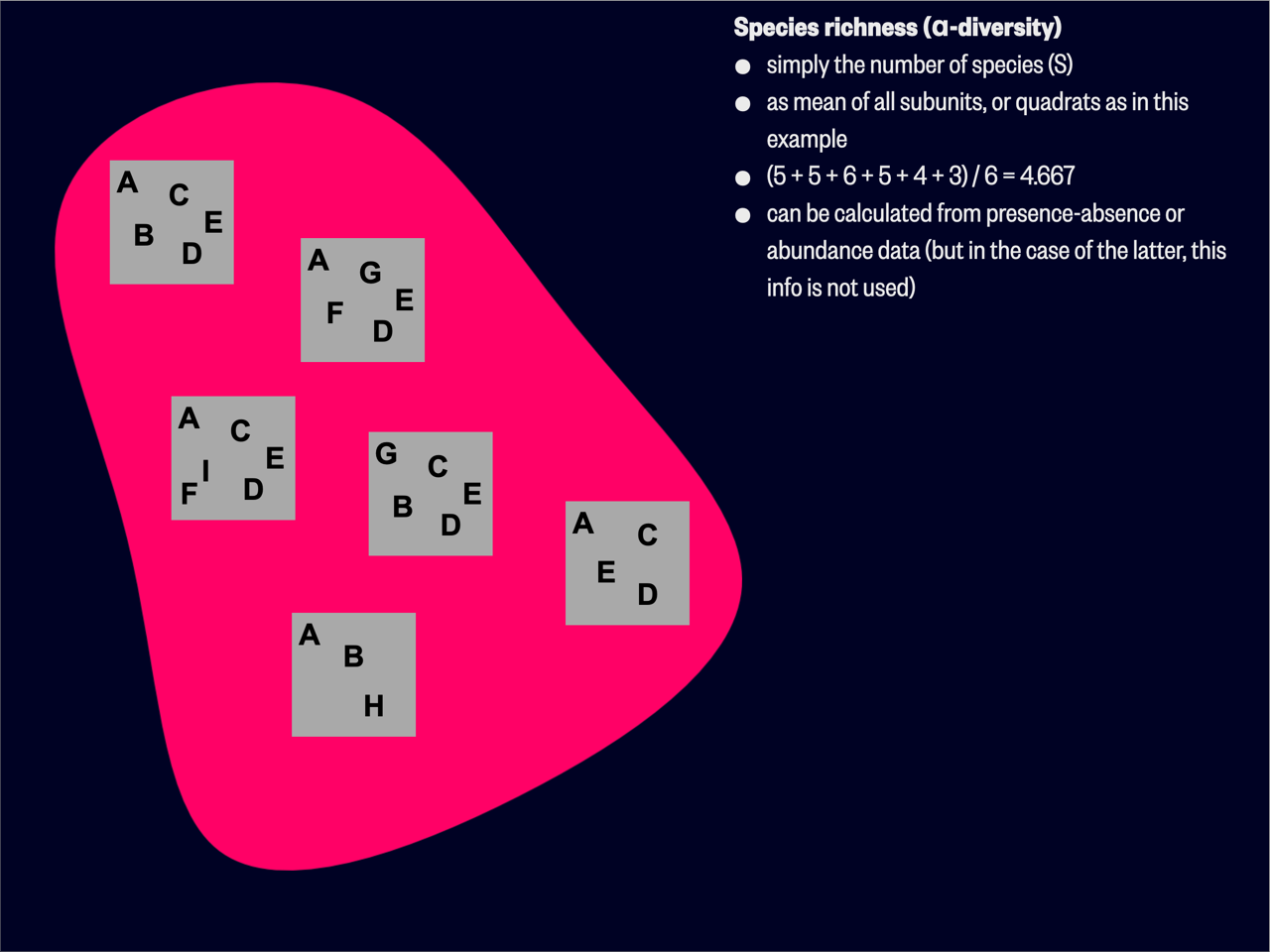
Alpha diversity quantifies the diversity of species within a specific, localised area or community. This could be a site, plot, quadrat, a field, or any other small unit of (typically) replication in the study. This measure provides information about the ecological structure and complexity of a given habitat at a fine scale.
There are several ways to represent \alpha-diversity. The simplest and most straightforward measure is species richness, which is simply a count of the number of different species present in the sampling area. Simply put, this is a list of species within the local scale. If we have multiple local scale sites, we can calculate the average species richness across all sites (Figure 1).
Species richness is easy to understand and implement, but it doesn’t account for the relative abundance of each species within the community. To address this limitation we make use of univariate indices. Shannon’s H’ (Shannon’s Diversity Index) and Simpson’s \lambda (Simpson’s Diversity Index) are such univariate diversity indices. These indices place various amounts of emphasis on the abundance and evenness of species present.
Choosing Shannon’s or Simpson’s is a bit controversial and it often depends on who is using it. According to Jari Oksanen, author of the vegan package in R, the choice between Shannon’s and Simpson’s index is a matter of personal preference. He writes:
Better stories can be told about Simpson’s index than about Shannon’s index, and still grander narratives about rarefaction (Hurlbert 1971). However, these indices are all very closely related (Hill 1973), and there is no reason to despise one more than others (but if you are a graduate student, don’t drag me in, but obey your Professor’s orders). In particular, the exponent of the Shannon index is linearly related to inverse Simpson (Hill 1973) although the former may be more sensitive to rare species.
Both Shannon’s H’ or Simpson’s \lambda can be applied to the local scale, or averaged across multiple sites to get a regional scale measure of the average \alpha-diversity. We will revisit Shannon’s H’ or Simpson’s \lambda lower down in this section as they also crop up in under the heading of Diversity Indices (another logical place to classify the same concepts).
\beta-Diversity (Variation in Diversity)
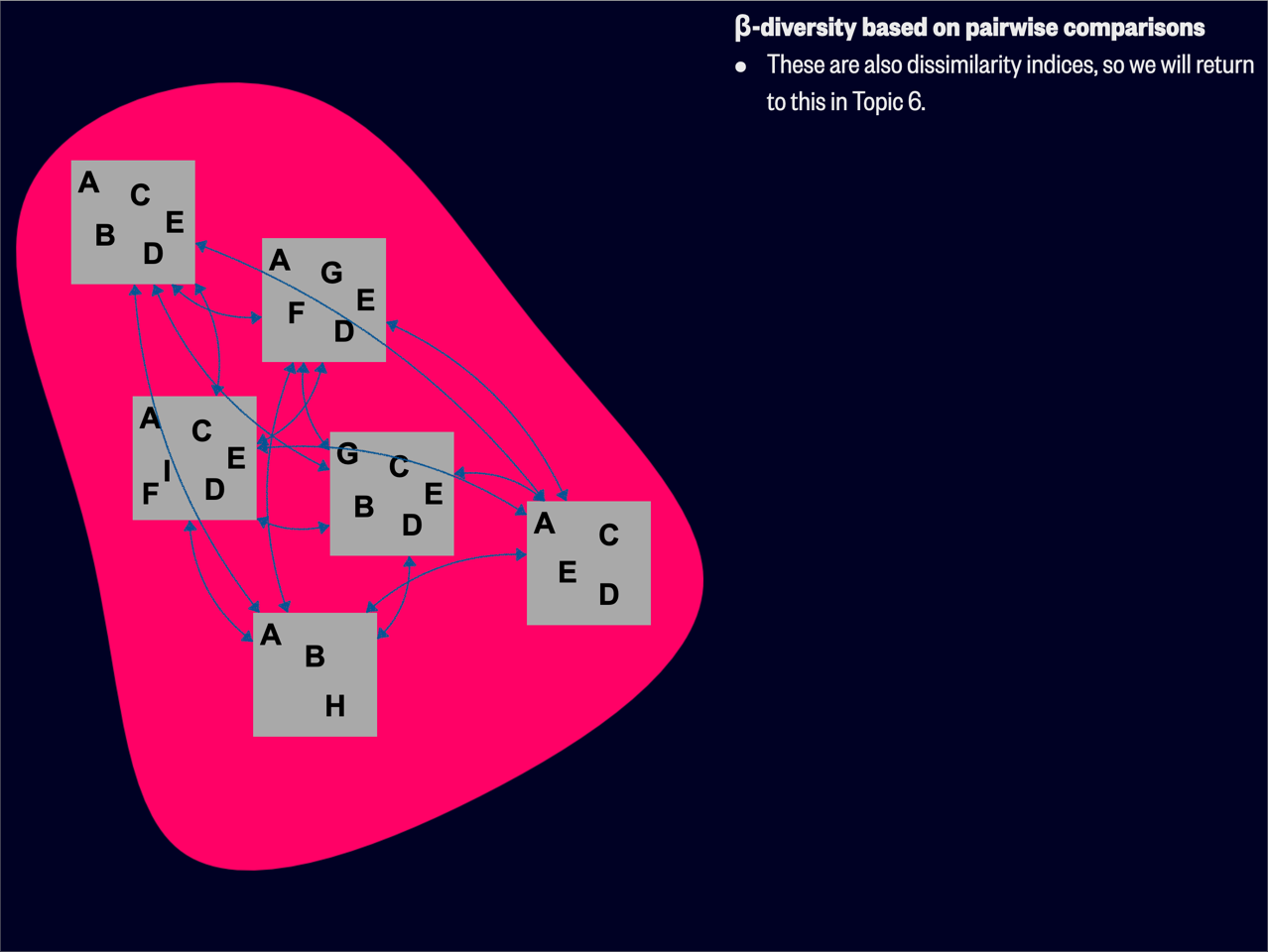
A related concept of diversity is one that considers the variation between sites (Figure 2). This is known as \beta-diversity. \beta-diversity refers to the measure of diversity between different communities or ecosystems within a larger region. It quantifies the variation in species composition from one habitat or site to another and captures the degree of differentiation or turnover of species across spatial scales. \beta-diversity helps to understand how species diversity is distributed across different environments and can indicate the impact of environmental gradients, habitat fragmentation, and ecological processes on community composition. It links local (\alpha-diversity) and regional (\gamma-diversity) scales and offers a processed-based view on biodiversity formation.
\beta-diversity has a long history in ecology and has undergone several conceptual revisions over the years. The concept was first introduced by Whittaker (1960) to describe the variation in species composition between different sites.
Whittaker’s initial idea was that of true \beta-diversity (hence it sometimes being called Whittaker’s \beta-diversity), which is often defined as the effective number of distinct communities in a region. It can be calculated as the ratio of \gamma-diversity to \alpha-diversity when these are expressed as Hill numbers or effective numbers of species. Mathematically, this is expressed as:
\beta = \frac{\gamma}{\alpha}
where \beta is true \beta-diversity, \gamma is the total diversity of the region, and \alpha is the mean diversity of the individual communities.
Another approach is absolute species turnover, which is a measure of the total amount of species change between communities or along environmental gradients. It can be calculated in various ways, but one common approach is to use the Whittaker’s \beta-diversity index:
\beta_w = \frac{S}{\alpha} - 1
where S is the total number of species in all communities combined (\gamma-diversity), and \alpha is the average number of species found in all the local scale samples that comprise the region.
This measure of turnover ranges from 0 (when all communities have identical species composition) to a maximum value that depends on the number of communities being compared. It provides a quantitative measure of how much species composition changes across communities or sites.
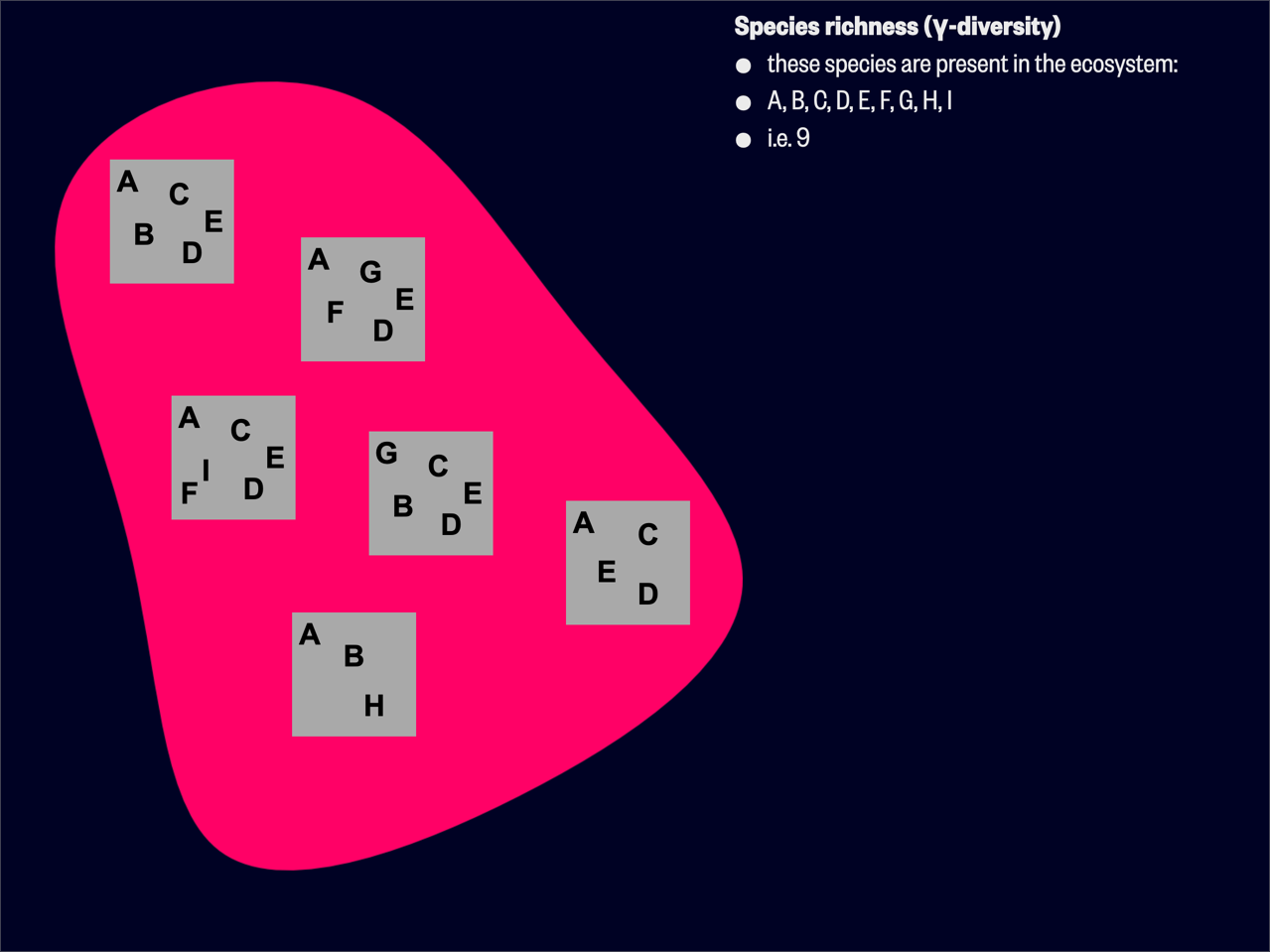
Contemporary views of \beta-diversity were developed by Nekola and White (1999), Baselga (2010), and Anderson et al. (2011). This information is encapsulated with pairwise matrices of dissimilarity indices (see the section below on dissimilarity indices where the various dissimilarity indices are presented in more detail) calculated for each pair of sites within the studied system. The broad implication is the same as how it was traditionally applied: that is, \beta-diversity describes how species formation (into communities) measured within the ecosystem of interest vary from place to place, e.g. between the various transects or quadrats used to sample the ecosystem. But, these modern interpretations of \beta-diversity extract from these views of habitat heterogeneity some deeper insights about the mechanisms responsible for driving the community formation process, viz. the role of gradients (Process 1: niche theory) and stochastic processes (Process 2: neutral theory).
Process 1: If a region comprises the species A, B, C, …, M (i.e. \gamma-diversity is 13), a subset of the regional flora captured by one quadrat might be species A, D, E. In another quadrat species A, D, F might be present. \alpha-diversity is three in both instances, and heterogeneity (and hence \beta-diversity) results from the fact that the first quadrat has species E, but the other has species F. In other words, here, we have the same number of species in both quadrats, but only two of the species are the same. The process responsible for this form of \beta-diversity is species turnover, \beta_\text{sim}. Turnover refers to processes that cause communities to differ due to species being lost or gained from section to section, i.e. the species composition changes between sections without corresponding changes in \alpha-diversity. The function beta() in the R package BAT calls this form of \beta diversity replacement and use the symbol \beta_{repl} (Cardoso et al. 2015).
Process 2: Consider again species A, B, C, …, M. Now we have a quadrat with species A, B, C, D, G, H (\alpha-diversity is six) but another quadrat has a subset of these species, e.g. only species A, B, G (\alpha-diversity three). Here, \beta-diversity is high even though the quadrats share some species, but the number of species differs among the quadrats (i.e. from place to place) due to one quadrat capturing only a subset of species present in the other. This form of \beta-diversity is called nestedness-resultant \beta-diversity, \beta_\text{sne}, and it refers to processes that cause species to be gained or lost, and the community with the lowest \alpha-diversity is a subset of the richer community. The function beta() in the R package BAT calls this form of \beta diversity *richness difference** and uses the symbol \beta_{rich} (Cardoso et al. 2015).
The above two examples show that \beta-diversity is coupled not only with the identity of the species in the quadrats but also \alpha-diversity—with species richness in particular.
We express \beta-diversity as nestedness-resultant, \beta_\text{sne}, and turnover, \beta_\text{sim}, components to be able to distinguish between these two processes. It allows us to make inferences about the two possible drivers of \beta-diversity. Turnover refers to processes that cause communities to differ due to species being lost or gained from section to section, i.e. the species composition changes between sections without corresponding changes in \alpha-diversity. The nestedness-resultant component implies processes that cause species to be gained or lost without replacement, and the community with the lowest \alpha-diversity is a subset of the richer community.
According to Nekola and White (1999) on p. 868, there are two causes of ecological distance decay. ‘Ecological’ is key to the first cause—it is environmental filtering results in a decrease in similarity as the distance between sites increases. We sometimes call this the niche difference model. Such patterns are typically visible along steep environmental gradients such as elevation slopes (mountains), latitude, or depth in the ocean, to name only three. It is also the dominant mechanism underlying island biogeography.
The second cause of distance decay sensu Nekola and White (1999) involves aspects of the spatial configuration, context of the habitats, and some temporal considerations. Here, the evolutionary differences between species—specifically around those traits that affect their ability to disperse—are more at play and are the primary influences of distance decay rates that might vary between species. Let us first consider some properties of a hypothetical homogeneous landscape. The landscape creates some impediment (resistance) to the propagation of some species (hypothetically species A, B, and C) across its surface, but which are less effective in impeding others (D, E, and F). For argument’s sake, all species (A, …, F) share similar environmental tolerances to the prevailing environmental conditions, so one can argue that the niche difference model (environmental filtering) does not explain distributional patterns. Given a particular founding or disturbance event, species D, E, and F will, in a relatively shorter period, be able to become evenly distributed (relatively similar abundances everywhere) across this landscape. However, the less vagile (in terms of dispersal ability), species A, B, and C will develop a steeper gradient of decreasing species abundances away from the founding populations (resulting from, for example, adaptive radiation). They will require more time to become homogeneously dispersed across the landscape. In this regard, historical events set up striking distributional patterns that can be mistaken for gradients, which exist because insufficient time has passed to ensure complete dispersal. Studying the influence of such past events is called ‘historical biogeography.’ In reality, landscapes are seldom homogeneous in their spatial template (e.g. there are hills and valleys), and variable dispersal mechanisms and abilities will interact with this heterogeneous landscape to form interesting patterns of communities. The ecologist will have an exciting time figuring out the relative importance of actual gradients vs those that result from evolved traits that affect their dispersal ability and interact with the environment. I have not said anything about ‘neutral theories’ (but which are seen in the \beta_\text{sne} form of \beta-diversity as in Smit et al. 2017), nor biological interactions that might affect community structure.
\gamma-Diversity (Regional Diversity)
While \alpha-diversity focuses on the local scale, representing the species richness within a specific area or community, the concept of species richness changes as we broaden our scope of observation. This brings us to the concept of \gamma-diversity, which refers to the overall diversity of a larger area or region encompassing multiple local-scale units of observation or quantification (Figure 3). The transition from \alpha- to \gamma-diversity occurs as we aggregate data from multiple sampling units or sites within a broader landscape or ecosystem. \gamma-diversity captures the total species diversity across all the local communities in a region. It is not merely the average \alpha-diversity or total \alpha-diversity aggregated over individual sites; rather, it reflects the combined diversity, including both the diversity within each local community (\alpha-diversity) and the diversity between communities (\beta-diversity).
Diversity Indices
A diversity index is a metric that quantifies species diversity within a community. While species richness simply refers to the number of species present, diversity indices also consider the relative abundances of these species. For instance, consider two communities: community A comprises 10 individuals of each of 10 species (totalling 100 individuals) and community B has 9 species with 1 individual each, and a 10th species with 91 individuals (also totalling 100 individuals). Which community is more diverse? To address this, diversity indices incorporate both richness and evenness information and provides a more comprehensive assessment of diversity than species richness alone.
Margalef’s Index
Margalef’s Index is a simple measure of species richness that accounts for the number of species in a community and the total number of individuals. The formula for Margalef’s Index is:
D = \frac{S - 1}{\ln(N)}
where S is the total number of species in the community, and N is the total number of individuals. A higher value of D indicates greater diversity.
Shannon’s Entropy
Shannon’s Entropy, or Shannon’s H’, comes out of the field of information theory and was developed by Claude Shannon. It measures the uncertainty or diversity within a system. It is a general measure of information content and is applicable to a variety of data types beyond species diversity, such as genetic diversity, linguistic diversity, or even the distribution of different types of land use in a landscape. The formula for Shannon’s H’ is as used by ecologists is:
H' = -\sum_{i=1}^{S} p_i \ln(p_i)
where S is the total number of species in the community, and p_i is the proportion of individuals belonging to species i. A higher H’ value indicates greater diversity, with values typically ranging from 0 to about 4.5, rarely exceeding 5 in extremely diverse communities. We use this index to help us understand the evenness and richness of species within a community, and it is used when we need to emphasise the contribution of rare species.
Simpson’s Indices
Simpson’s Indices are a group of related diversity measures developed by Edward H. Simpson. These indices focus on the dominance or evenness of species in a community, giving more weight to common species and being less sensitive to species richness compared to Shannon’s H’.
Simpson’s Dominance Index
Simpson’s Dominance Index (\lambda) measures the probability that two individuals randomly selected from a sample will belong to the same species. The formula for Simpson’s Dominance Index is:
\lambda = \sum_{i=1}^{S} p_i^2
where S is the total number of species, and p_i is the proportion of individuals belonging to species i. Values range from 0 to 1, with higher values indicating lower diversity (higher dominance). A value of 1 represents no diversity (only one species present), while a value approaching 0 indicates very high diversity.
Simpson’s Diversity Index
To make the index more intuitive we prefer to use Simpson’s Diversity Index, which is calculated as:
1 - \lambda = 1 - \sum_{i=1}^{S} p_i^2
This form ensures that the index increases with increasing diversity. Values range from 0 to 1, with higher values indicating higher diversity.
Simpson’s Reciprocal Index
Another common form is Simpson’s Reciprocal Index, calculated as:
\frac{1}{\lambda} = \frac{1}{\sum_{i=1}^{S} p_i^2}
This index starts with a value of 1 as the lower limit, representing a community containing only one species. The upper limit is the number of species in the sample (S). Higher values indicate greater diversity.
Simpson’s Indices are less sensitive to species richness and more sensitive to evenness compared to Shannon’s Entropy. They are useful when you want to give more weight to common species in your diversity assessment.
Gini Index
The Gini Index, or Gini Coefficient, should be fimiliar to all South Africans—South Africa is infamous for having the highest Gini Coefficient in the world. The Gini Index is a measure of inequality within a distribution, and is typically used in economics to assess income or wealth inequality. Since its purpose is to evaluate disparity, it is also suited to ecological systems because, here too, the distribution in abundance differs among species. The formula for the Gini Index is:
G = \frac{\sum_{i=1}^{N} \sum_{j=1}^{N} |x_i - x_j|}{2N^2 \bar{x}}
where N is the total number of observations, x_i and x_j are the values of the observations, and \bar{x} is the mean of the values. In ecological studies, a high Gini Index indicates a large disparity in species abundances, with few species dominating the community, whereas a low Gini Index suggests a more even distribution of individuals among species.
Herfindahl-Hirschman Index (HHI)
The Herfindahl-Hirschman Index (HHI) is a measure of market concentration commonly used in economics to assess the level of competition within an industry. It is calculated as the sum of the squares of the market shares of all firms in the market. Ecologists sometimes use the HHI to assess species dominance or the concentration of individuals within species. The formula for HHI is:
HHI = \sum_{i=1}^{N} s_i^2
where N is the total number of species, and s_i is the proportion of individuals belonging to species i. Here, a higher HHI indicates a higher concentration of individuals in a few species, signifying lower diversity. Conversely, a lower HHI reflects a more even distribution of individuals across species, indicating higher diversity.
Here’s a corrected and improved version of the text:
Ecological Resemblance
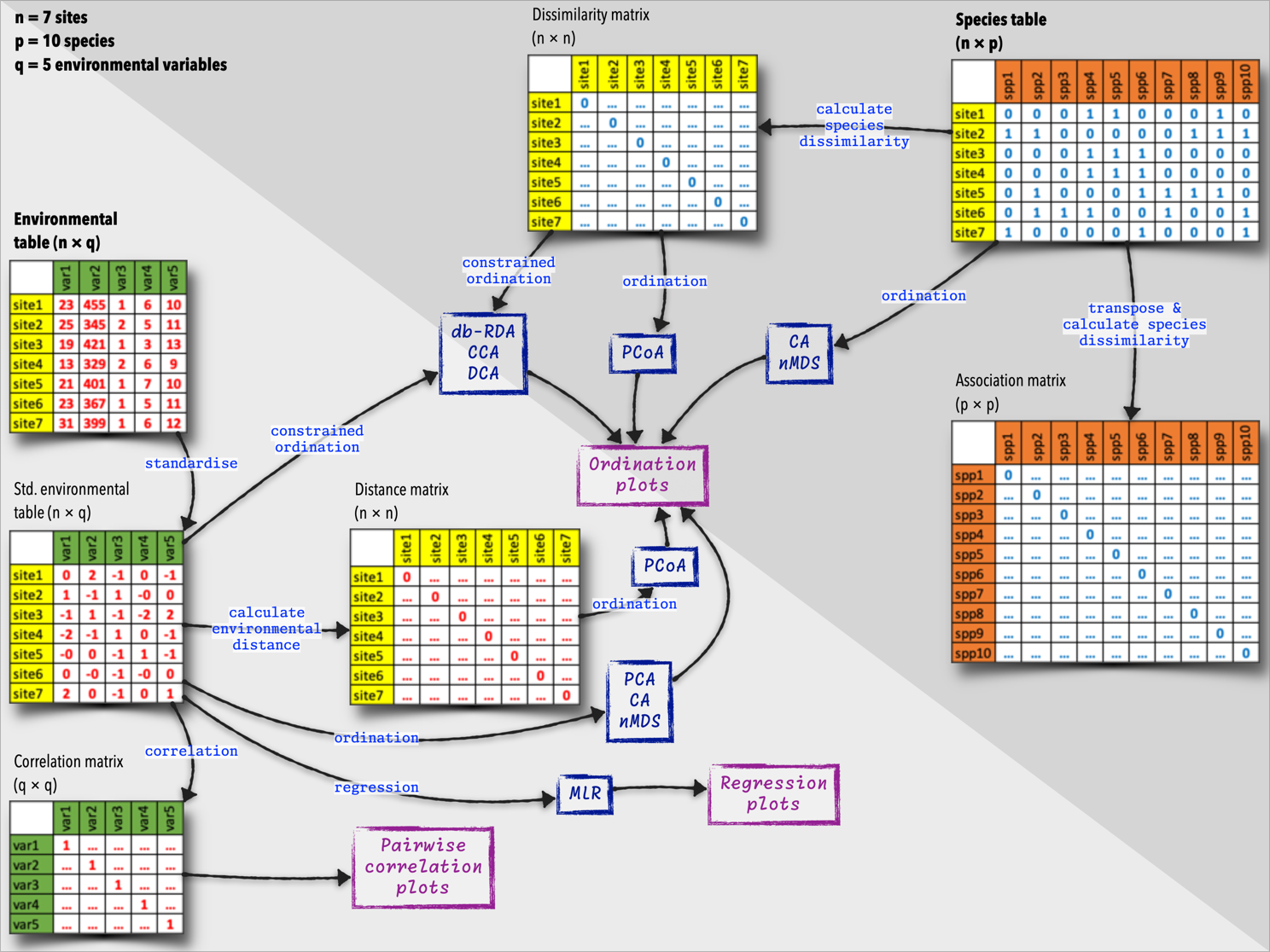
Resemblance matrices are mathematical representations used to quantify the similarity or dissimilarity between pairs of samples, communities, or ecological sampling units based on various criteria such as species composition, abundance, functional traits, phylogenetic relatedness, or environmental properties. Well-structured raw data about species composition typically come in the form of a table with rows representing sites or samples, and columns representing species. Similarly, data about environmental variables are structured as a table with rows representing sites or samples, and columns representing environmental variables.
The diagram below (Figure 4) summarises the species and environmental data tables, and what we can do with them. These tables are the starting points of many additional analyses, and we will explore some of these deeper insights later in this module.
Although we often use the terms ‘matrix’ and ‘table’ interchangeably, in this book I use matrix to refer to a mathematical object with rows and columns and with the cell content derived from calculations of distances and dissimilarities. In these situations they tend to be square and symmetrical. I then use the term table to refer to a more general data structure, also with rows and columns, but here representing samples or sites (as rows) and columns representing species or environmental variables. My use of ‘table’ generally refers to the raw data we use as a starting point for our calculations (including of the matrices).
This is my notations and authors such as Borcard et al. (2011), David Zelený, and Michael Palmer may not make this distinction and use both terms to refer to a rectangular data structure.
When the focus is on comparing sites (i.e., the information about objects in the rows of site × species or site × environment tables) based on their species composition or environmental characteristics, we call this type of analysis an R-mode analysis. Such resemblance matrices typically manifest as square matrices, with rows and columns representing the samples or units being compared.
Other cases of square resemblance matrices include: i) Species-by-species matrices (association matrices), where both rows and columns represent species, and the values in the matrix represent the association between each pair of species. ii) Environmental-by-environmental matrices (correlation matrices), where both rows and columns represent environmental variables, and the values in the matrix represent the correlation between each pair of variables. In these cases, the focus falls onto the information initially contained in the columns (species or descriptors) of the sites × species table or the sites × environmental variables table. This is called a Q-mode analysis.
Environmental resemblance matrices, or environmental distance matrices, are used to quantify the similarity between pairs of sites based on their environmental variables. They can also be used in more advanced analyses, such as various kinds of ordinations and clustering. These matrices have zeros down the diagonal, as the distance between a site and itself is zero. The subdiagonal values are typically the same as the superdiagonal values, as the dissimilarity between samples i and j is the same as the dissimilarity between samples j and i, i.e., the matrices are symmetrical. The off-diagonal values represent the distance between pairs of sites, with higher values indicating greater dissimilarity.
In species dissimilarity matrices (species resemblance matrices), the values represent the degree of dissimilarity between each pair of samples. Dissimilarity matrices are characterised by a diagonal filled with zeros, because the dissimilarity between a sample and itself is zero. The off-diagonal values represent the dissimilarity between pairs of samples, with higher values indicating greater dissimilarity. They are also symmetrical for the same reasons given for the environmental matrices. Species dissimilarity matrices are used in various multivariate analyses, such as cluster analysis, ordination, and diversity partitioning.
Legendre and Legendre (2012) provide a full chapter (Chapter 7) on ecological resemblance, including an in-depth look at the various kinds of ‘association coefficients,’ which is what we will cover next. The next two sub-sections will thus introduce a few frequently used association coefficients to study species dissimilarity and environmental distances across the landscape.
Environmental Distance
Sometimes we need to quantify the environmental similarities or differences between sampling sites, such as plots, quadrats, or transects. This is typically achieved through the use of distance matrices (one kind of resemblance matrix), which provide an overall view of how all the sites relate to one another. These matrices are derived from data tables containing information on environmental variables (sites in rows and variables in columns).
There are several kinds of distance metrics available for use with environmental data. Regardless of which index one chooses, the resulting matrix provides pairwise differences (or distances) or similarities in a metric that relates to the ecological distance between all sites (and which might also link to their community composition, which is the thing we are trying to determine). Such pairwise matrices are foundational for various multivariate analyses and can reveal patterns in ecological data that might not be apparent from raw measurements of individual variables alone.
Euclidean distance is in my experience the commonly used in spatial analysis. It defined as the straight-line distance between two points in Euclidean space. In its simplest form, it applies to a planar area such as a graph with x- and y-axes, but it can be extended to higher dimensions. In two or three dimensions, it gives the Cartesian distance between points on a plane (x, y) or in a volume (x, y, z), and this concept can be further extended to higher-dimensional spaces. Euclidean distance conforms to our intuitive physical concept of distance, making it useful for applications like measuring short geographic distances between points on a map. However, over large distances on Earth’s surface, Euclidean distance loses accuracy due to the Earth’s spherical shape. In such cases, great circle distances, calculated using formulas like the Haversine formula, provide more accurate measurements.
Mathematically, Euclidean distance is calculated using the Pythagorean theorem. This method squares the differences between coordinates, which means that single large differences become disproportionately important in the final distance calculation. While this property makes Euclidean distance useful for environmental data, where it effectively calculates the ‘straight-line distance’ between two points in multidimensional space (with each dimension representing an environmental variable), it is ill suited to species data.
The Euclidean distance between two points A and B in a n-dimensional space is calculated as:
d_{jk} = \sqrt{\sum_{i=1}^{n} (j_i - k_i)^2}
where j_i and k_i are the values of the i-th variable at points j and k, respectively.
Other distance metrics are the Mahalanobis Distance, Manhattan Distance, Canberra Distance, Gower Distance, and Bray-Curtis Dissimilarity. I’ll not discuss them here and you can refer to Chapter 3 in the book by Borcard et al. (2011) for more information. Additionally, vegan’s vegdist() function does a very good job of providing a wide range of distance metrics and you can find a discussion of many of them in the function’s help file, which you can access as ?vegan::vegdist.
Species Dissimilarities
Ecological similarity between sites is fundamentally tied to their species composition, which is a function of both species richness and abundance. Sites that share similar species compositions are considered ecologically similar and exhibit a low dissimilarity metric. The factors influencing this similarity are complex and influenced by many properties of the environment and processes operating there.
As we have already seen, the degree of similarity between sites can be attributed to measurable environmental differences (i.e. hopefully captured in the environmental distance matrices we saw above) that directly influence species composition. These might include variables like soil type, climate, or topography. However, similarity can also be affected by unmeasured, often overlooked influences that are not immediately apparent or easily quantifiable. Additionally, some degree of variation may simply be attributed to ecological ‘noise’—random fluctuations or stochastic events that affect species distributions.
It is our role to disentangle these various influences and determine the primary drivers of similarity or dissimilarity among sites. To aid in this analysis, we use a class of matrices known as dissimilarity matrices (a type of resemblance matrix). These matrices quantify the dissimilarity between sites based on their species composition.
Various indices have been developed to compare the composition of different groups or communities. These diversity indices quantify how different or similar groups are based on their attributes, primarily species richness and/or relative abundances. While the simplest application is to compare the species composition of two sites, these indices can be extended to compare multiple groups or communities. They are core to the study of β-diversity, which examines the variation in species composition among sites within a geographic area.
I’ll present the Bray-Curtis dissimilarity as an example, which is a widely-used metric for comparing species composition between two sites. For abundance data, it is calculated as follows:
d_{jk} = \frac{\sum_i |x_{ij} - x_{ik}|}{\sum_i (x_{ij} + x_{ik})}
where x_{ij} and x_{ik} are the abundances of species i (the columns) at sites j and k (the rows) respectively.
For presence-absence data, the Bray-Curtis dissimilarity simplifies to:
d_{AB} = \frac{A+B-2J}{A+B-J}
where J is the number of species present in both sites being compared, A is the number unique to site A, and B is the number unique to site B.
The Bray-Curtis dissimilarity ranges from 0 (indicating identical species compositions) to 1 (indicating completely different compositions). This metric can be used to construct dissimilarity matrices for multivariate analyses, where each cell in the matrix represents the ecological distance between a pair of sites based on their species composition.
In practice, these dissimilarity indices and distances can be calculated using the vegan R package’s vegdist() function. Refer to ?vegan::vegdist for information and a deeper look.
Common dissimilarities suited to presence-absence data are the Jaccard Dissimilarity, Sørensen-Dice index, and Ochiai index. For abundance data, we have already seen the Bray-Curtis dissimilarity, but you also have the Morisita-Horn index, which is also commonly used. The Raup-Crick index is used to compare the dissimilarity between two groups to the expected dissimilarity between two random groups, whilst the Chao-Jaccard and Chao-Sørensen indices are probabilistic versions of the Jaccard and Sørensen indices that account for unseen shared species.
References
Reuse
Citation
@online{j._smit2024,
author = {J. Smit, Albertus},
title = {Lecture 2b: {Metrics} of {Environmental} {Distance} \&
{Species} {Diversity}},
date = {2024-07-22},
url = {http://tangledbank.netlify.app/BDC334/L02b-biodiversity.html},
langid = {en}
}